C1b: B−¯B mixing, CP violation, and Lifetimes
| Principal Investigators | |
|---|---|
| Prof. Ulrich Nierste | Karlsruhe Institute of Technology |
| Prof. Matthias Steinhauser | Karlsruhe Institute of Technology |
Subject
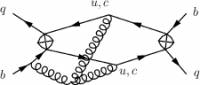
The project addresses lifetimes differences between heavy hadrons containing a heavy quark Q=b,c and a light quark q=u,d,s and semileptonic CP asymmetries of Bd and Bs decays. The lifetime (or width) difference between the two mass eigenstates of the neutral Bq meson, q=d,s, and the semileptonic CP asymmetry aCP(Bq→Xℓν) both originate from ¯Bq and involve the decay matrix element Γq12. The Heavy Quark Expansion (HQE) expresses these quantities as an expansion in ΛQCD/mQ and αs(mQ), where mQ (with Q=b,c) is the heavy quark mass. For instance, the width difference ΔΓ between different Q-flavoured hadrons has the schematic form ΔΓ∝1m3Q∑j[αs4π]jΓ(j)3+1m4Q∑j[αs4π]jΓ(j)4+….
Key features of studied quantities:
- same technique (HQE) but different sensitivity to new physics
- simultaneously test formalism and probe new physics
- theory uncertainties larger than experimental errors
- NLO perturbative uncertainty larger than or comparable to hadronic uncertainty
In this project we aim at the calculation of NNLO (three-loop) corrections to Γ(j)3 and of NLO (two-loop) corrections to Γ(j)4 for the mentioned lifetimes differences and CP asymmetries.
Project Topics
- Γq12 to NNLO for mc=0
- will reduce perturbative uncertainty of leading-power contribution to ΔΓs from ∼10% to ∼3%
- requires solution of new three-loop integral families
- Γq12 at order αs/mb
- needed to reduce overall uncertainty in ΔΓq/ΔMq well below 10\%
- τ(B+)/τ(Bd) and τ(Ξ0b)/τ(Ξ−b) at orders α2s and αs/mb
- tests the formalism (HQE and lattice calculations)
- Charm hadron lifetimes
- tests the HQE at order 1/mQ
- τ(Bs)/τ(Bd) and τ(Λb)/τ(Ξ0b)
- probes new physics in penguin coefficients
- Γq12 to NNLO at order m2c/m2b
- NNLO accuracy for adfs, which probes new physics in e.g. b→dˉqq decays
- Phenomenological studies
- devise judicious combinations to reduce hadronic uncertainties
- propose new observables